GAIN:Missing-Data-Imputation-using-Generative-Adversarial-Nets
一篇来自 ICML’18 的关于数据补全的work,文章链接 Link
摘要
我们根据Generative Adversarial Nets提出了一个数据补全方法:Generative Adversarial Imputation Nets (GAIN)。其中,generator (G) 根据已有的真实观测值向量,有条件的进行补全,并输出一个完整的向量。Discriminator (D) 根据完整向量尝试区分真实数据和补全数据。为了确保 D 令 G 学习期望的数据分布,我们向 D 提供了 hint vector。Hint 向D提供了原始数据缺失的部分信息,用来提升D对后续插补部分的关注。hint 保证了G 能够根据真实数据分布进行学习。我们在不同的数据集上测试了GAIN,结果显示其效果显著优于当前SOTA
背景
简单背景,数据缺失无处不在
数据缺失的类型:MCAR, MAR,MNAR
当前方法:
- discriminative
- MICE
- Miss Forest
- matrix completion
- generative
- Expectation Maximization
- DAE
- GAN
drawback: …
GAIN:
generator: 尽可能准确地进行数据补全, 尽可能增大D的分类误差
discriminator: 区分补全和真实数据, 尽可能的减少分类loss(某个entry是补全 or 真实的分类)
就像一个正常的GAN一样去train
问题定义
$\chi = \chi_{1} \times \dots \times \chi_{d}$
${\mathbf{X}} = (X_{1}, \dots, X_{d})$
${\mathbf{X}}$ 中连续或离散的在对应位置占有 $\chi$ 的值,分布为 $P({\mathbf{X}})$
${\mathbf{M}} = (M_{1}, \dots, M_{d})$
${\mathbf{M}}$ 中的值为 0/1
${\tilde{\chi}} = \chi_{i} \cup \{*\}$
其中 $*$ 不在$\chi$ 中, 表示未观测值
所以,可以得到新的表示:
$ \tilde{\chi} = \tilde{\chi}_{1} \times \dots \times \tilde{\chi}_{d} $
${\tilde{\mathbf{X}}} = ({\tilde{X}}_{1}, \dots, {\tilde{X}}_{d}) \in {\tilde{\chi}}$
$\mathbf{M}$ 能表示 $\mathbf{X}$ 中哪些是真实观察的,额能够从 ${\tilde{\mathbf{X}}}$ 中恢复得到 $\mathbf{M}$
Method
在这部分中,作者根据GANs,使用 $P(\mathbf{X}|{\tilde{\mathbf{X}}} = {\tilde{x}^{i}})$ 来描述GAIN
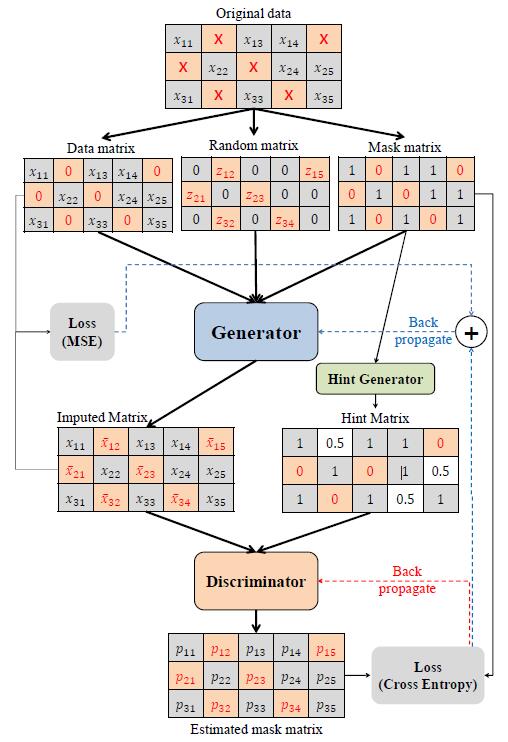
Generator
以原始残缺数据 data matrix, $\tilde{\mathbf{X}}$, 随机噪声 random matrix $\mathbf{Z}$, mask matrix $\mathbf{M}$作为输入,输出一个补全矩阵 imputed matrix
其中 $\overline{\mathbf{X}}$ 是补全后的生成数据矩阵,包含了新生成的残缺数据和原始数据(所以这里生成的原始数据要替换)
$\hat{\mathbf{X}}$ 则表示真正的补全矩阵, 包含 生成补全数据 和 原始观测数据
Discriminator
以补全矩阵 和 hint matrix 作为输入,得到 estimated mask matrix,并与原始的 mask matrix 进行 Cross Entropy.
IDEA
很强的一个work,
将imputation作为一个生成数据问题,同时完整的进行了问题定义
对于Generator进行了完整定义,
Discriminator比较有趣的,将这个imputation视为分类,判别生成数据的真假(👍)
GAIN:Missing-Data-Imputation-using-Generative-Adversarial-Nets

