Multivariate-Time-Series-Imputation-with-Generative-Adversaria-Networks

一篇来自 NIPS’18 的关于数据补全的work，文章链接 Link

background

将缺失数据处理分为三类, 确切来说，直接删除残缺、线性/插0补全、机器学习方法。然而将这些方法不能很好的考虑两个observation间的时序关系

method

• 传统的GAN存在训练困难的问题，因此这里采用了WGAN
• 传统的RNN变种对于残缺数据这种，存在两个观测值差距较远的情况不适用。因此设计了新的 Gated Recurrent Unit for data Imputation (GRUI)

Defination

对于一个时序，具有两个维度：时间 $\textbf{T} = (t_{0}, t_{1},…,t_{n-1})$, 每个时间点上的特征维度$d$。所以时序观测值$\textbf{X} = (x_{t_{0}},…,x_{t_{i}},…,x_{t_{n-1}})$.

$$\textbf{X}=\left[\begin{array}{cccc} 1 & 6 & \text { none } & 9 \\ 7 & \text { none } & 7 & \text { none } \\ 9 & \text { none } & \text { none } & 79 \end{array}\right],$$ $$T=\left[\begin{array}{c} 0 \\ 5 \\ 13 \end{array}\right]$$

定义mask matrix $\textbf{M} \in {\mathbb{R}^{n \times d}}$ 来表示当前$\textbf{X}$的残缺情况,$M^{j}_{t_{i}} = 1$则表示$X^{j}_{t_{i}}$存在.

$$\textbf{M}=\left[\begin{array}{cccc} 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \end{array}\right].$$

定义 time lag matrix $\delta \in {\mathbb{R}^{n \times d}}$来记录当前值和最后有效值的距离.

$$\delta_{t_{i}}^{j}=\left\{\begin{array}{ll} t_{i}-t_{i-1}, & M_{t_{i-1}}^{j}==1 \\ \delta_{t_{i-1}}^{j}+t_{i}-t_{i-1}, & M_{t_{i-1}}^{j}==0 \& i>0 \\ 0, & i==0 \end{array}\right.$$ $$\delta = \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 5 & 5 & 5 & 5 \\ 8 & 13 & 8 & 13 \end{array}\right].$$

定义 time decay vector $\beta$ 来控制过去观测值的影响，$\beta \in (0, 1]$，${\delta}$的值越大，对应的$\beta$越小

$${\beta}_{t_{i}}=1 / e^{\max \left(\mathbf{0}, \textbf{W}_\boldsymbol{\beta}{\delta}_{t_{i}}+\textbf{b}_{\beta}\right)}$$

GRUI

与GRU相似:

$$h_{t_{i-1}}^{\prime}=\beta_{t_{i}} \odot h_{t_{i-1}}\\$$ $$\mu_{t_{i}}=\sigma\left(\boldsymbol{W}_{\mu}\left[\boldsymbol{h}_{t_{i-1}}^{\prime}, \boldsymbol{x}_{t_{i}}\right]+\boldsymbol{b}_{\mu}\right)\\$$ $$\boldsymbol{r}_{t_{i}}=\sigma\left(\boldsymbol{W}_{r}\left[\boldsymbol{h}_{t_{i-1}}^{\prime}, \boldsymbol{x}_{t_{i}}\right]+\boldsymbol{b}_{r}\right)\\$$ $$\tilde{\boldsymbol{h}}_{t_{i}}=\tanh \left(\boldsymbol{W}_{\tilde{h}}\left[\boldsymbol{r}_{t_{i}} \odot \boldsymbol{h}_{t_{i-1}}^{\prime}, \boldsymbol{x}_{t_{i}}\right]+\boldsymbol{b}_{\tilde{h}}\right)\\$$ $$\boldsymbol{h}_{t_{i}}=\left(\mathbf{1}-\boldsymbol{\mu}_{t_{i}}\right) \odot \boldsymbol{h}_{t_{i-1}^{\prime}}+\boldsymbol{\mu}_{t_{i}} \odot \tilde{\boldsymbol{h}}_{t_{i}}$$

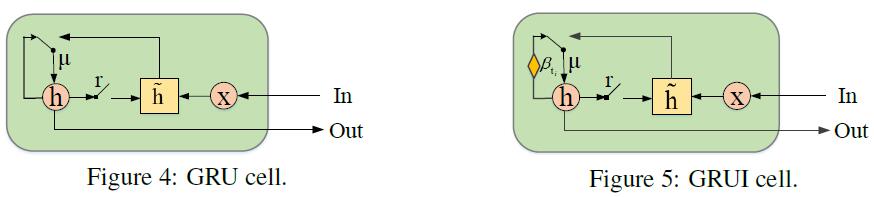
GAN

D: 首先是 GRUI，然后跟着 Linear和dropout；
在输入原始不完全时序特征时到D时，$\delta$的每一行内不相同；而在输入至G时，每一行内相同。
G：也是由GRUI和Linear构成。

定义了两个Loss

masked reconstruction loss. 表示$G(z)$应该和原始残缺$x$足够接近

$$L_{r}(\boldsymbol{z})=\|\boldsymbol{X} \odot \boldsymbol{M}-G(\boldsymbol{z}) \odot \boldsymbol{M}\|_{2}.$$

discriminative loss.表示令$G(z)$尽可能真实.

$$L_{d}(\boldsymbol{z})= - D(G(z)).$$

最终，loss function可以表示为

$$L_{imputation}(z) = L_{r}(z)+\lambda L_{d}(z)$$

$\lambda$为超参。

对于原始时序特征x，我们从高斯分布中降采样一个 z，并放入G得到G(z)。在训练至收敛后，我们将$x$的残缺值替换为下式

$$\boldsymbol{x}_{i m p u t e d}=\boldsymbol{x} \odot \boldsymbol{M}+(\mathbf{1}-\boldsymbol{M}) \odot G(\boldsymbol{z})$$

Experiement

在一个医疗数据集和一个空气质量数据集进行实验。

结果看起来还行.

Idea

看起来只是将GAN和GRU修改之后变得适用于imputation 这个task,

亮点：

• 整个结构设置的比较合理
• 从mask matrix的角度生成合适的G(z)
• GRUI也相较于普通的GRU更实用.
• 整个GAN框架为之后基于GAN进行imputation提供了基础

不足：

• 背景故事不太有说服力，为什么那些传统的model不太work
• WGAN和GNA的区别性在method中并没有提出太多